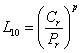A GÖRDÜLŐCSAPÁGYAK MÉRETEZÉSE

A gördülőcsapágyak szilárdsági méretezésének célja a terhelés elviselésére alkalmas méretű csapágyak kiválasztása. A csapágy nagyságának meghatározására szolgáló módszer függ a csapágy terhelés alatti mozgásállapotától. Más a számítási módszer akkor, ha a csapágy a terhelés alatt forog, és ismét más akkor, ha nyugalmi állapotban van, illetve kis fordulatszámú forgó- vagy lassú lengőmozgást végez. Az előbbi esetben dinamikus, az utóbbiban pedig statikus igénybevételről van szó. A dinamikus igénybevétel az anyag kifáradását, a statikus pedig maradó alakváltozását idézi elő. Ennek megfelelően beszélünk élettartamra, illetve maradó alakváltozásra történő méretezésről. Ez utóbbi a maximális terhelhetőség megállapítását jelenti.

 Méretezés élettartamra

Az élettartam fogalma

A terhelés alatt forgómozgást végző gördülőcsapágy működő felületén (a gördülőpályákon vagy a gördülőtesteken) bizonyos idő eltelte után kifáradási jelenségek lépnek fel. A kifáradás a gördülőfelületek alatti hajszálrepedés képződéssel kezdődik, majd a repedések tovaterjedve gödrösödéshez, ún. pittingképződéshez vezetnek. Az adott csapágy élettartamán a kifáradási tünetek jelentkezéséig megtett körülfordulások számát értjük. Az egyes csapágyak élettartama egymástól nagyon eltérő lehet. Mivel az élettartam valószínűségi változó, a konkrét csapágy élettartamának kiszámítása lehetetlen. Azért, hogy az élettartamra történő méretezés mégis elvégezhető legyen, bevezették a névleges élettartam fogalmát.

A gördülőcsapágyak L₁₀ névleges élettartama az az élettartam, amelyet nagyszámú, azonos méretű és típusú, azonos körülmények között működő gördülőcsapágy 90%-a elér, vagy túlél. Nevezik ezt a 90%-os megbízhatósághoz tartozó élettartamnak is. A névleges élettartamot a csapágyak jó részének élettartama számottevően meghaladja. Az átlagos, vagy közepes élettartam a névlegesnek ötszörösére tehető, azaz a csapágyak fele a névleges élettartam ötszörösét éri el. Az L₁₀ névleges élettartamot többnyire millió körülfordulásban határozzuk meg. Megadható azonban állandó fordulatszám esetén, a teljesített üzemórákban mérve is, ez esetben a jele L_10h.

A dinamikus alapteherbírás

A dinamikus alapteherbírás - amint a neve is mutatja - nem egyéb, mint a csapágy dinamikus terheléssel szembeni ellenálló képessége. Eszerint a C dinamikus alapteherbírás radiális csapágyaknál az a tisztán sugárirányú, axiális csapágyaknál pedig tisztán tengelyirányú, állandó, egyenletesen, az axiális csapágyaknál ezenkívül központosan is ható terhelés, amelynek hatására a csapágy névleges élettartama 1 millió körülfordulás.

A dinamikus alapteherbírás a csapágyalkatrészek geometriai méretei, valamint anyaga figyelembevételével számítható és minden csapágyra jellemző érték. A dinamikus alapteherbírás számszerű értékei a mérettáblázatokban megtalálhatók.

Az élettartam- egyenlet és alkalmazása

A radiális gördülőcsapágy névleges élettartama, terhelése és dinamikus radiális alapteherbírása között az alábbi összefüggés áll fenn:

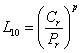(millió körülfordulás)                                4.1

ahol

L₁₀       a névleges élettartam, millió körülfordulásban

C_r         a dinamikus radiális alapteherbírás kN-ben,

P_r         a dinamikus radiális egyenértékű terhelés kN-ben,

p          élettartam-kitevő, amelynek értéke

golyóscsapágyaknál p = 3,

görgőscsapágyaknál p = 10/3

A gyakorlati élet igényeihez közelebb kerülünk, ha a csapágyak élettartamát millió körülfordulás helyett üzemórákban fejezzük ki. Ha a csapágy n percenkénti fordulatszáma állandó, akkor az L₁₀ üzemórákban mért élettartam a következő kifejezésből számítható:

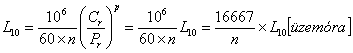                  4.2

Az üzemi hőmérséklet befolyása a dinamikus alapteherbírásra

Az átedzhető,    nagy     tisztaságú         krómacélból      készült  gördülőcsapágyak dinamikus alapteherbírásának meghatározásánál a gondos hőkezelés által biztosított szövetszerkezetet és

keménységet tételezzük fel. Nyilvánvaló, hogy olyan hőhatás, amely e szövetszerkezetet megváltoztatja, befolyással van a dinamikus alapteherbírásra, sőt a méretekre is. Ez a hatás végleges, mert a szövetszerkezet megváltozása gyakorlatilag irreverzíbilis. A nagy hőmérsékletek dinamikus alapteherbírást csökkentő hatását oly módon vesszük figyelembe, hogy annak a mérettáblázatokban megadott értékeit a csapágy üzemelése közben tartósan elért legnagyobb t (°C) hőmérséklettől függő, a 4.1. táblázatból kiolvasható f, hőmérsékleti tényezővel megszorozzuk. Az élettartam számítást ezzel a módosított dinamikus alapteherbírással kell végrehajtani.

Táblázat 4.1 A hőmérsékleti tényező értékei

A módosított élettartam-egyenlet

Az (4.1) és (4.2) képletekkel számított névleges élettartam a tapasztalatokkal kielégítő mértékű egyezést mutat, azaz a terhelés hatását az összefüggések a gyakorlati igényeknek megfelelő pontossággal írják le, minden szokásos csapágyazási esetben, amikor hagyományos összetételű, tisztaságú, gondosan hőkezelt acélt használunk a csapágygyártáshoz, a beépítést körültekintően hajtjuk végre, és az üzemeltetés - beleértve a kenést is - szabatos feltételek között folyik.

Minden olyan körülmény és adottság, amely a feltételektől eltér, az élettartam megrövidülését vagy meghosszabbodását okozhatja, ezért szükség lehet adott esetben arra, hogy a csapágy élettartamára befolyást gyakorló egyes tényezők hatását pontosabban vegyük figyelembe.

Erre a célra került bevezetésre az L_na módosított élettartam fogalma. A módosított élettartam az anyagok különleges tulajdonságait, a speciális üzemeltetési feltételeket, a tetszés szerint választott és megkövetelt megbízhatóságot veszi figyelembe. Kiszámítása az

vagy egyszerűbben az

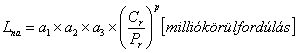                                4.3

L_na = a₁ a₂ a₃ L₁₀ [millió körülfordulás]

összefüggéssel lehetséges, ahol

a₁         élettartam-valószínűségi tényező,

a₂         anyagtényező,

a₃         üzemeltetési feltételek tényezője.

Az élettartamot ebben az esetben is ki lehet fejezni üzemórákban a (4.2) összefüggés segítségével.

A módosított élettartam-számítás alkalmazásának az a feltétele, hogy a csapágy terhelését pontosan számba vegyük és az üzemeltetési körülményeket is jól ismerjük. Nyilvánvaló, hogy abban az esetben, ha az élettartam-valószínűség 90%, a szokásos tulajdonságú csapágyacélt használjuk, és az üzemi feltételek is szokványosak, akkor

a₁ = a₂ = a₃ = 1, és a (4.3.) képlet azonos az (4.1.) képlettel.

Az élettartam-valószínűségi tényező (a₁) értékei a 4.2. táblázatban találhatók.

Látható, hogy milyen rohamosan csökken a csapágyak számításba vehető élettartama, ha a

megbízhatóságukkal szembeni követelményt fokozzuk.

Táblázat 4.2 Az élettartam valószínűségi tényező értékei

Az anyagtényezővel (a₂) csak különleges anyagok használata esetén kell számolni. Jól hőkezelt, hagyományos összetételű gördülőcsapágy-acél alkalmazásánál a₂ = 1 érték vehető figyelembe.

Az üzemeltetési feltételek tényezője (a₃) elsősorban a kenés hatásosságát van hivatva számba venni. Magában foglalja a kenési körülmények, a kenőanyag vegyi összetétele, a kenőanyag adalékok, a kenőanyag tisztasága, valamint a kenőanyag víztartalmának hatását. Az élettartamot pozitív és negatív értelemben egyaránt befolyásolhatja.

Tekintettel arra, hogy a kenési hiányosságok jobb anyaggal nem kompenzálhatók, azaz elégtelen kenés esetén a₂ sem lehet 1-nél nagyobb, a két tényező nem független egymástól, ezért az a₂ és a₃ tényezőket egy közös, az anyag és az üzemeltetési körülmények hatását együttesen kifejező a₂₃ tényezőbe szokás összevonni. Ezzel a módosított élettartam-képlet az alábbi, gyakorlati számításra is használható alakot ölti.

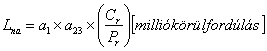
vagy

 [millió körülfordulás]

Az a₂₃ tényező szabványos gördülőcsapágy-acélnál használatos értékei a  viszkozitás hányados függvényében a 4.3. táblázatban találhatók meg, ahol:

v a tényleges használt kenőolaj viszkozitása

v₁ az adott üzemi hőmérsékleten és fordulatszámon szükséges kenőolaj viszkozitás.

Táblázat 4.3 Az anyag és üzemeltetési körülmények hatását kifejező tényező értékei

A v és v₁ érték megválasztási szempontjai a Gördülőcsapágyak kenése című fejezetben található.

A módosított élettartam számításnál a csapágy tönkremenetelének okaként pusztán az anyag kifáradását tekintettük. Az így meghatározott élettartam azonban csak akkor lehet azonos a csapágy tényleges működési idejével, ha a kenési állapot a csapágy használata közben végig állandó, a számításnál figyelembe vett terhelés és fordulatszám a valóságossal azonos, a kenőanyag viszkozitásának megállapításánál az üzemi hőmérsékletet jól becsültük meg, a szennyeződéseket működés közben is távol tartottuk a csapágytól, és kenési hiba vagy kopás nem korlátozza a csapágy működőképességét.

Dinamikus egyenértékű csapágyterhelés

A radiális, illetve az axiális csapágyak P dinamikus egyenértékű terhelése, az az állandó, egyenletesen ható, radiális csapágyaknál tisztán sugárirányú, illetve axiális csapágyaknál tisztán tengelyirányú, központosan ható képzelt erő, melynek hatására a csapágy névleges élettartama ugyanakkora, mint az üzem közben fellépő, nagyságát és irányát tekintve változó, dinamikus hatásokkal kísért erő esetén.

A dinamikus egyenértékű terhelést a csapágy erőközéppontján átmenő terhelőerőből kell kiszámítani. A csapágy erőközéppontja a csapágy hatásvonalának és tengelyének metszéspontja. Szimmetrikusnak tekinthető csapágyak esetében az erőközéppont a csapágy geometriai középpontjával esik egybe. Kúpgörgős csapágyaknál az erőközéppontnak a külső gyűrű széles homlokához viszonyított helyzetét a mérettáblázatok tartalmazzák.

A gördülőcsapágyak hatásvonala alatt azt az egyen est értjük, amelyre illeszkedik a gyűrűk és gördülőtestek között átadódó erőrendszer eredője. A hatásvonalhoz viszonyítva aszimmetrikus gördülőtesteket tartalmazó csapágyak (pl. kúpgörgős csapágy esetében a hatásvonal a külső gyűrű gördülőpályájára merőleges. A hatásvonal és a csapágy tengelyére merőleges sík által bezárt szög az a hatásszög.

Az O erőközéppontot, a hatásvonalat, a hatásszöget, valamint az F eredő terhelő erőnek a csapágy tengelyére merőleges síkkal bezárt β terhelési szögét a 4.1 ábra szemlélteti.

Radiális golyóscsapágyak dinamikus radiális egyértékű terhelése állandó terhelés és fordulatszám esetén:

        (4.5)

Az X és Y értékeket a radiális hézagtól függően a 4.4 táblázatból kell venni, figyelembe véve az F_a/C_or, viszonyt. A terhelés axiális komponense csak akkor növeli az axiális terhelést, ha az F_a/F_r viszony nagyobb az "e" terhelési határszámnál.

Táblázat 4.4 Egyenértékű terhelés számításának tényezői

Radiális egysoros kúpgörgős csapágyak dinamikus egyenértékű terhelése állandó terhelés és fordulatszám esetén:

P_r=F_r                ha F_a/F_r ≤ e

P_r=0,4F_r+X F_a   ha F_a/F_r > e

Az e és Y tényezők értékeit a mérettáblázat tartalmazza.

A kúpgörgős csapágyaknál a radiális terhelés hatására járulékos axiális erő keletkezik, mert a külső gyűrű futópálya a csapágytengelyhez képest szöget zár be. Ez az erő a tengely másik csapágyára - ami rendszerint szintén kúpgörgős csapágy - mint reakcióerő hat, amit az egyenértékű terhelés számításánál figyelembe kell venni.

A 4.2 ábrán látható O és X elrendezés esetében az egyenértékű terhelés meghatározásához az F_a axiális terhelést a járulékos erők és a K_a külső tengelyirányú terhelés figyelembevételével a 4.5 táblázat útmutatásai szerint lehet számítani. Az ábrák szerinti csapágyelrendezéseknél mindig annak a csapágynak a jele 1, amely a külső K_a tengelyirányú terhelést felvenné, ha sugárirányú erők nem hatnának.

4.2 ábra

Táblázat 4.5

Terhelési viszonyok		Fa axiális terhelés az egyenértékű terhelés meghatározásához
		1 jelű csapágy	2 jelű csapágy
I.			-
II			-
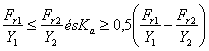
III.		-

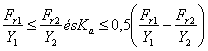
Azoknál az eseteknél, ahol összefüggést nem adtunk meg, a járulékos erőt nem kell figyelembe venni, mert F_a/F_r < e

Itt a P_r = F_r egyenlőség érvényes.